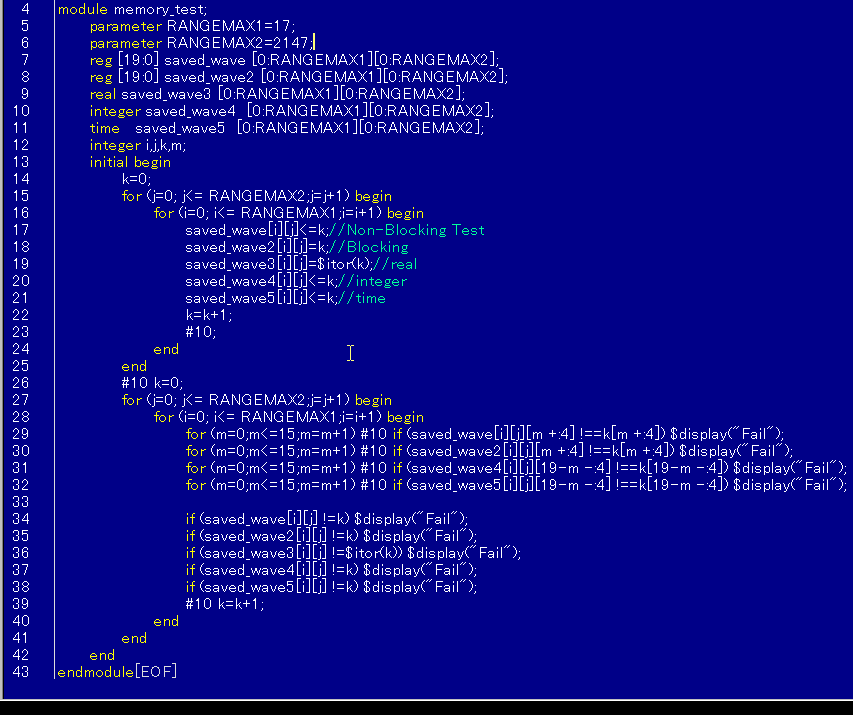
8.1.2 string について
8.演算子
| オペランドになりえる種類 | 例 | 備考 |
| 定数 (realも含む) | 3'b001、24, 16'hzzzz | REALで出来る演算子は限られる。 |
| Net | wire [3:0] a; a | |
| Variables : reg,integer,time,real,and realtime | reg [3:0] b; b | |
| Net ビットセレクト | a[1] | |
| Variable ビットセレクト: reg,integer,and time | b[3] | |
| Net パートセレクト | a[2:1] | |
| パートセレクト: reg,integer,and time | b[3:1] | |
| アレーの要素 | reg [7:0] c[0:3]; c[3] | |
| ファンクションで上記のタイプを返すもの |
オペレーター
| {} {{}} | 連接 | Real |
| +-*/** | 算術演算、**は、Verilog2001 Power演算 | 可 |
| % | モジュロ演算 | |
| > >= < <= | 比較演算 | 可 |
| ! | 論理否定 | 可 |
| && | 論理積 | 可 |
| || | 論理和 | 可 |
| == | Logical equality | 可 |
| !== | Logical inequality | 可 |
| === | Case equality | |
| !== | Case inequality | |
| ~ | Bit-wise NOT | |
| & | Bit-wise AND | |
| | | Bit-wise OR | |
| ^ | Bit-wise EXOR | |
| ^~or ~^ | Bit-wise equivalence | |
| & | Reduction AND | |
| ~& | Reduction nand | |
| | | Reduction or | |
| ~| | Reduction nor | |
| ^ | Reduction xor | |
| ~^ or ^~ | Reduction xnor | |
| << | Logical Shift Left | |
| >> | Logical Shift Right | |
| <<< | Arithmatic Shift Left(Verilog2001動作的には<<と同じ) | |
| >>> | Arithmatic Shift Right(Verilog2001) | |
| ?: | Ternary ( C言語に同じ) | 可 |
| or | イベントのOR | 可 |
演算子の優先度
| + - ! ~ (単項) | 最上位 |
| ** | |
| */% | |
| + - (2項) | |
| << >> <<< >>> | |
| < <= > >= | |
| == != === !== | |
| & ~& | |
| ^ ^~ ~^ | |
| | ~| | |
| && | |
| || | |
| ?:(conditional operator) | 最下位 |
8.1 オペランド
8.1.1 bit select とpart select
宣言レンジを越えたときは、xが返ります。
| reg [3:0] a; reg b; integer i; initial begin i=4; b=a[i];//宣言レンジを越えているのでxが返る end |
パートセレクトは2種類あります。
一つ目は、
| vect[msb_expr : lsb_expr] |
でmsb_expr と lsb_expr共、定数でなければなりません。
二つ目は、Verilog2001仕様で、
| reg [15:0] big_vect; reg [0:15] little_vect; big_vect[lsb_base_expr +: width_expr] little_vect[msb_base_expr +: width_expr] big_vect[msb_base_expr -: width_expr] little_vect[lsb_base_expr -: width_expr] |
で、width_exprは、定数でなければなりませんが、lsb_expr、msbexprは、変数でOKです。

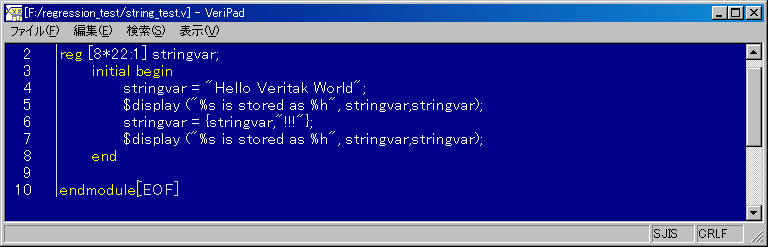
8.1.2 string について

この実行結果は、次のようになります。右詰めにされて左側は0padされます。
Hello Veritak World is stored as 00000048656c6c6f205665726974616b20576f726c64 Hello Veritak World!!! is stored as 48656c6c6f205665726974616b20576f726c64212121 |
8.2 Integer Numberについて
integer IntA;
IntA = -12 / 3; //−4になります。 The result is -4.
IntA = -’d 12 / 3; // 1431655761になります。
IntA = -’sd 12 / 3; //Verilog2001 -4になります。
IntA = -4’sd 12 / 3; //Verilog2001 1になります。 4'sd12=.1100,符号付なので、-4 Unary演算で、-(-4)=>4 4/3=1
8.3 算術演算子
| a+b |
| a-b |
| a*b |
| a/b |
| a%b |
8.3.1 モジュロオペレータ
| 演算 | 結果 | |
| 10 %3 | 1 | |
| 11 %3 | 2 | |
| 12 %3 | 0 | |
| -10 %3 | -1 | 符号は、第一オペランドを取る |
| 11 %-3 | 2 | 符号は、第一オペランドを取る |
| -4'sd12%3 | 1 | -4'sd12は、4です。(Verilog2001) |
8.3.2 算術表現の符号
| タイプ | Signed/Unsigned |
| net | signed 宣言のないnetはUnsigned |
| reg | signed 宣言のないnetはUnsigned |
| signed net | Signed |
| signed reg | Signed |
| integer | Signed |
| time | Unsigned |
| real,realtime | Signed,floating point |
8.3.3 除算の符号(Verilog2001)
reg [15:0] regA;
reg signed [15:0] regS;
integer intA;
initial begin
intA = -4'd12;
regA = intA / 3; // expression result is -4,intA is an integer data type, regA is 65532
if (regA !=65532 ) $display("Fail1");
regA = -4'd12; // regA is 65524
if (regA !=65524) $display("Fail2");
intA = regA / 3; // expression result is 21841
if (intA !=21841) $display("Fail3");
intA = -4'd12 / 3;// expression result is 1431655761. -4’d12 is effectively a 32-bit reg data type
if (intA !=1431655761) $display("Fail4");
regA = -12 / 3; // expression result is -4, -12 is effectively an integer data type. regA is 65532
if (regA !=65532) $display("Fail5");
regS = -12 / 3; // expression result is -4. regS is a signed reg
if (regS !=-4) $display("Fail6");
regS = -4'sd12 / 3;// expression result is 1. -4’sd12 is actually 4. The rules for integer division yield 4/3==1
if (regS !=1) $display("Fail7");
end
8.3.4 <<< >>>について(Verilog2001)
算術シフト演算子 <<<は、<<と同じです。(アセンブラ表記が違っても、マシンコードが同じであるように) >>>シフト演算子は、第一パラメータがsignedであるときだけ算術シフト動作を行い、unsigned
のときは、>>(論理シフト)と同じ動作になります。
なお、Rotational演算子は、Verilogではありません。
<例>
reg [7:0] xu;
reg signed [7:0] xs;
initial begin
xu = 8'b1100_0000;
xs = 8'b1100_0000;
xu = xu >>> 3;//xuは、unsignedなので、8'b0001_1000になります。
xs = xs >>> 3;//xsは、signedなので、8'b1111_1000になります。
xs = xu >>> 3;//8'b0001_1000になります。LHSに依存しません。
xu = xs >>> 3;//8'b1111_1000になります。LHSに依存しません。
end // initial begin
8.3.5 符号のルール(Verilog2001)
例
reg [15:0] a;
reg signed [7:0] b;
initial
a = b[7:0]; // b[7:0] は、 unsigned パートセレクトよって、unsignedなのでゼロ拡張される。
Realを含んだら、結果はReal
Unsigngedを含んだら、結果はunsigned
全てのオペランドがsignedなら、signedになります。ただし、前述ルールが優先されます。
Note:
符号付と符号なしの違い
乗算で見ましょう。ソースです。
`define DIFF_CHECK
module signed_mul_test;
parameter integer width=3;
parameter integer mul_width=width*2;
integer i,j;
reg signed [width-1:0] as,bs;
reg [width-1:0] a,b;
reg [mul_width-1:0] mul;
reg signed [mul_width-1:0] muls;
wire [mul_width-1:0] mulw=a*b;
wire signed [mul_width-1:0] mulws=as*bs;
initial begin
for (i=0;i<2**width-1;i=i+1) begin
a=i;
as=i;
for (j=0;j<2**width-1;j=j+1) begin
b=j;
bs=j;
mul=a*b;
muls=as*bs;
#10;
`ifdef DIFF_CHECK
if (mul !=muls) begin
$display("Unsigned a =%d[%b] b =%d[%b] mul =%d[%b] ",a,a,b,b,mul,mul);
$display("Signed as=%d[%b] bs=%d[%b] muls=%d[%b] ",as,as,bs,bs,muls,muls);
$display("");
end
`endif
if (mul !=mulw) $display("Fail");
if (muls !=mulws) $display("Fail");
end
end
end
endmodule
実行結果です。
F:\regression_test\signed_mul_test.v(2)::signed_mul_test
Verilogのシミュレーションの準備が完了しました。スタートは,Goボタンを押してください。
------------- シミュレーションを開始します。--------------------
Unsigned a =1[001] b =4[100] mul = 4[000100]
Signed as= 1[001] bs=-4[100] muls= -4[111100]
Unsigned a =1[001] b =5[101] mul = 5[000101]
Signed as= 1[001] bs=-3[101] muls= -3[111101]
Unsigned a =1[001] b =6[110] mul = 6[000110]
Signed as= 1[001] bs=-2[110] muls= -2[111110]
Unsigned a =2[010] b =4[100] mul = 8[001000]
Signed as= 2[010] bs=-4[100] muls= -8[111000]
Unsigned a =2[010] b =5[101] mul =10[001010]
Signed as= 2[010] bs=-3[101] muls= -6[111010]
Unsigned a =2[010] b =6[110] mul =12[001100]
Signed as= 2[010] bs=-2[110] muls= -4[111100]
Unsigned a =3[011] b =4[100] mul =12[001100]
Signed as= 3[011] bs=-4[100] muls=-12[110100]
Unsigned a =3[011] b =5[101] mul =15[001111]
Signed as= 3[011] bs=-3[101] muls= -9[110111]
Unsigned a =3[011] b =6[110] mul =18[010010]
Signed as= 3[011] bs=-2[110] muls= -6[111010]
Unsigned a =4[100] b =1[001] mul = 4[000100]
Signed as=-4[100] bs= 1[001] muls= -4[111100]
Unsigned a =4[100] b =2[010] mul = 8[001000]
Signed as=-4[100] bs= 2[010] muls= -8[111000]
Unsigned a =4[100] b =3[011] mul =12[001100]
Signed as=-4[100] bs= 3[011] muls=-12[110100]
Unsigned a =4[100] b =5[101] mul =20[010100]
Signed as=-4[100] bs=-3[101] muls= 12[001100]
Unsigned a =4[100] b =6[110] mul =24[011000]
Signed as=-4[100] bs=-2[110] muls= 8[001000]
Unsigned a =5[101] b =1[001] mul = 5[000101]
Signed as=-3[101] bs= 1[001] muls= -3[111101]
Unsigned a =5[101] b =2[010] mul =10[001010]
Signed as=-3[101] bs= 2[010] muls= -6[111010]
Unsigned a =5[101] b =3[011] mul =15[001111]
Signed as=-3[101] bs= 3[011] muls= -9[110111]
Unsigned a =5[101] b =4[100] mul =20[010100]
Signed as=-3[101] bs=-4[100] muls= 12[001100]
Unsigned a =5[101] b =5[101] mul =25[011001]
Signed as=-3[101] bs=-3[101] muls= 9[001001]
Unsigned a =5[101] b =6[110] mul =30[011110]
Signed as=-3[101] bs=-2[110] muls= 6[000110]
Unsigned a =6[110] b =1[001] mul = 6[000110]
Signed as=-2[110] bs= 1[001] muls= -2[111110]
Unsigned a =6[110] b =2[010] mul =12[001100]
Signed as=-2[110] bs= 2[010] muls= -4[111100]
Unsigned a =6[110] b =3[011] mul =18[010010]
Signed as=-2[110] bs= 3[011] muls= -6[111010]
Unsigned a =6[110] b =4[100] mul =24[011000]
Signed as=-2[110] bs=-4[100] muls= 8[001000]
Unsigned a =6[110] b =5[101] mul =30[011110]
Signed as=-2[110] bs=-3[101] muls= 6[000110]
Unsigned a =6[110] b =6[110] mul =36[100100]
Signed as=-2[110] bs=-2[110] muls= 4[000100]
---------- シミュレーションを終了します。time=490----------
どちらかに、MSB1が立ったとき、符号付と符号なしの結果が違うことがわかります。MSBは、符号ビットですから当たり前ですね。
8.3.6 expressionの評価ステップ
8.3.7 式の評価ステップ
8.3.8 signed expressionにおけるxとzについて(Verilog2001)
signed を拡張するとき、符号項(msb項)が、xならxが、zならzが拡張されます。 unsignedなら、ゼロが拡張されます。
8.3.9 ビット幅について
式の代入においては、LHSビット幅も含めて最大のビット幅で評価されます。
<例>
reg [15:0] a, b; // 16-bit regs
reg [15:0] sumA; // 16-bit reg
reg [16:0] sumB; // 17-bit reg
sumA = a + b; // expression evaluates using 16 bits
sumB = a + b; // expression evaluates using 17 bits
RHSは、全く同じですが、LHSがそれぞれ、16ビット、17ビットになっているために、下のa+bは、符号なし拡張が行われ
sumB={1'b0,a} +{1'b0,b};
と等価になります。
ビット幅で注意することがあります。
<例>
reg [15:0] a, b, answer; //
answer = (a + b) >> 1; //うまく動かない??
a+bは、16ビット、answerも16ビットなので、a+bは、16ビット幅で評価されます。したがってOverflowを生じる可能性がありますが、式の評価ビット幅としては、16ビットで評価され、その後、1ビットシフト動作になります。この例の対策として、
answer = (a + b+0) >> 1; //うまく動くが..
0を追加する手が例示(LRM)されています。デシマル0は、少なくとも32ビット以上であることが保証されます。全体のオペレーションビット幅は、32ビット幅(以上)になります。従ってOverflowすることはない、、となっています。シミュレータ上ではその通りなのですが、論理合成で、必要でないビット幅まで、合成してしまうことが考えられますのでお勧めしません。最初から、Overflowまで考慮したビット幅にするべきでしょう。
たとえば、
reg [16:0] temp;
reg [15:0] answer;
temp={1'b0,a}+{1'b0,b};//17bitで式を評価させる。overflow させない。
answer=temp >>1;//
という答案になります。
注意するべきなのは、LHSとRHSのビット幅が異なるときです。Verilog のルールは、
|
VHDLなら、LHSとRHSが一致しないとコンパイルエラーになりますが、Verilogではエラーになりません。バグの温床になりえるのでできる限りLHSとRHSのビット幅を一致させて書く方が望ましいと思います。Lintツール(VeritakのLint オプション)でCheckするのも方法の一つです。
8.3.9.1 SelfDetermined ビット幅
上記の例は、LHSまで含めた最大ビット幅で評価されましたが、代入がない場合、たとえば、$display("%b",a&b)の a&b項は、SelfDeterminedのビット幅になります。SelfDeterminedビット幅は次の規則により決定されます。
| Expression | Bit length | 備考 |
| Unsized 定数 | Integerと同じ幅になります | 通常は、32ビット幅ですが、シミュレータの実装によります。もし、32ビット以上のビット幅のexpressionの一部だったら、 MSBがxならx、zならzが拡張される。そうでなければ(0または1なら、)、sgiendならsigned拡張,unsignedならゼロ拡張がなされる。 |
| Sized定数 | Size項で指定される通り | |
| i op j, ここでopは: + - * / % & | ^ ^~ ~^ |
max(L(i),L(j)) | Binary Operator |
| + - ~ | L(i) | Unary Operator |
| i op j, ここで opは === !== == != && || >> =< <= |
1 bit | オペランドは、max(L(i),L(j)) |
| op i,ここで opは、& ~& | ~| ^~ ~ ^ ^~ ! | 1 bit | Reduction演算、 全てのオペランドは、Selfdetermined |
| i op j,ここで op は、 >> << ** >>> <<< |
L(i) | jは、Selfdetermined |
| i ?j :k | max(L(j),L(k)) | iは,Selfdetermined |
| {i,...,j} | L(i)+..+L(j) | 全てのオペランドは、Selfdetermined |
| {i{j,..,k}} | i * (L(j)+..+L(k)) | 全てのオペランドは、Selfdetermined |
ここで、L(i)は、オペランドiのビット幅になります。
<例 >
module bitlength();
reg [3:0] a,b,c;
reg [4:0] d;
initial begin
a = 9;
b = 8;
c = 1;
$display ("answer = %b", c ? (a&b) : d);
end
endmodule
シミュレータは、 01000と表示しましたか?
a,bのビット幅より、dのビット幅の方が大きいですから、5ビット幅になります。従ってa&bの演算の前にビット拡張が行われ5ビットで評価される為です。
8.4 Ternary Operator
a ? b : c で、aがxやzだった場合はどうなるのでしょうか?
それは、下表になります。両方共、0/1でなかったら、残り全てのケースでxになります。
| ? | 0 | 1 | x | z |
| 0 | 0 | x | x | x |
| 1 | x | 1 | x | x |
| x | x | x | x | x |
| z | x | x | x | x |